Take a Test Article Library CEEJ Home Submit an Article Contact CEEJ
Article # 0026
Wood Structural Panel Box Headers
By James A. Lacy, P.E.
August, 2006
Abstract
The purpose of this paper is to describe a minimum set of calculations necessary for a wood structural panel box header for residential wood-frame construction. Three main issues control the structural design of headers: allowable deflection, allowable moment, and allowable shear. Example calculations, and a simplified approach using APA’s Design and Fabrication of Glued Plywood-Lumber Beams Appendix B tables are presented.
Disclaimer
Neither the author nor publisher is responsible for the use of this information. The accuracy or completeness of any information published is not guaranteed and neither the author nor publisher shall be responsible for any errors, omissions, or damages arising out of the use of this information. Additionally, construction is inherently risky due to the heterogeneity of wood products and the variability of work methods and quality control.
Problem
Load-bearing headers in residential wood-frame construction distribute forces around wall openings such as windows and doors. Locales who have chosen to utilize the International Residential Code (IRC) have the option to follow the prescriptive approach given in Section R602.7.1 for field construction of wood structural panel box headers. However, locales who are following the Uniform Building Code (UBC) do not have a prescriptive wood structural panel box header. The UBC addresses headers in Section 2320.11.6. For openings less than four feet across, the header must be a minimum of two nominal 2x’s securely connected together, or the equivalent cross section of nominal 4x wood.
For locales who have energy codes which require insulated headers, an engineered header will be required.
The purpose of this paper is to describe a minimum set of calculations necessary for a wood structural panel box header for residential wood-frame construction.
Theory
Three main issues control the structural design of headers: allowable deflection, allowable moment, and allowable shear.
Most building codes allow a deflection of a structural member to L/360. Separately, interior sheetrock allows a maximum of L/240. Brick veneer may only tolerate a deflection of L/960. So the selection of allowable deflection will depend on the interior and exterior finishes, the code structural minimum, and other additive deflections such as foundation movement.
Since the wood structural panel box header will be designed as a symmetrical section, the controlling factors for allowable moment are: the allowable working stress of the flange lumber parallel to the grain, and the depth of the header. The depth of the header will essentially determine the moment of inertia.
The main concern for shear stress is the horizontal shear in the plywood webs of the structural panel box header. Control over this issue will be the selection of plywood thickness, and grade of plywood. Vertical shear at the bearing ends should not be a major problem.
Example
Assumptions
The parameters for this example are a single-family residence, two-story, 2x6 wood-framing 24-inch on-center, 32 feet from load-bearing wall to load-bearing wall. There is no snow or seismic loading. Roof loading is 30 psf live and 7 psf dead on a gable roof. There is no attic storage; the attic is insulated at the ceiling. Attic loading is 10 psf live and 10 psf dead. The second floor ceiling is supported by trusses bearing only on the outside walls. Loading on the second floor is 30 pounds per square foot live and 10 pounds per square foot dead. The second floor is supported by trusses bearing on the outside walls and one interior wall. Loads are summarized as:
|
|
Live Load psf |
Dead Load psf |
|
Wind |
16 |
|
|
Roof |
30 |
7 |
|
Attic |
10 |
10 |
|
2nd Floor |
30 |
10 |
Sometime during the life of the structure, there will be a brief wind loading event of 90 mph. Mean roof height is 22 feet, on open terrain, for an Exposure C factor of 1.32. Roof pitch is 9:12, or 37 degrees. Wind loading will be 12.1 psf times 1.32 for 16 psf downward wind loading.[i]
The example wood structural panel box header will depart from the prescriptive IRC header. The IRC header has the plywood applied externally to the wood framing. Because this example uses sheathing in a shearwall design, the header will have the plywood applied within the envelope of the 2x6 framing. 2x4 lumber, two 15/32" plywood spacers, a 15/32" plywood web, and an opposite 19/32" plywood web will precisely match the 5.5" width of nominal 2x6 lumber. In this way, the headers may be assembled on a table prior to framing. The headers then become light-weight interchangeable components.
The headers will be further simplified. The top elevation of outside doors will define the top elevation of windows. Therefore, all headers will be the same depth. Design depth is 12 inches. This example will use only the loading seen at the first floor headers, since that is a worse case than the second floor headers.
This paper uses the Allowable Stress Design (ASD) convention, as that is the convention used by the works consulted. However, the 2005 National Design Specification for Wood Construction now uses both ASD and Load and Resistance Factor Design (LRFD).
Moments
A simplified approach is to treat the header bearing spacing at four feet, and the floor truss bearing on the center of the header as a point load. Even though that model is not entirely correct, since the point load is resting on double top plates, it is a conservative representation. Maximum acting moment M is then calculated as PL/4; here P is 1824 pounds without wind loading, and 2336 pounds during wind loading. Since L equals 4, acting M maximum is P in foot-pounds.
Computed maximum allowable bending moment is the additive of the flange M (2x4) and the web M (plywood). The flange provides most of the inertia. The symmetrical section flange allowable bending moment is calculated by:
M = Ft' In
_____
0.5h
where
M = Allowable bending moment in inch-pounds
Ft' = Allowable controlling working stress parallel to the grain of the flange lumber psi
In = Net moment of inertia of flange material in the section (inch4)
h= Depth of header inches
Ft' = Ft x CF x CD
where
CF = Size factor adjustment for flange lumber, National Design Specification[ii]
CD = Load duration factor adjustment for plywood or flange lumber, National Design Specification[iii]
Moment contribution by the plywood webs requires looking up values from the APA’s Plywood Design Specification. Because of the cross-plys, the moment of inertia can not be calculated as a solid object. Table 2, column 4 contains the areas needed for further computation. Fb may be found in Table 3. However, the contribution is substantially less than that of the flange.
Calculation of the maximum allowable bending moment is simplified by using APA’s Design and Fabrication of Glued Plywood-Lumber Beams. Appendix B tables give a preliminary starting point for moment and shear stresses. This example will substitute values for the 2x4 flange orientation; Spruce-Pine-Fir (SPF) No.2 2x4 instead of select Douglas Fir-Larch; and 15/32" plywood not rated structural 1. This calculation for the allowable moment may be summarized as:
Mtotal = (Mflange x (I/I) x (Ftno2/Ftselect) x Cd) + (Mweb x Cd x Note3 x Note4)
|
3563 |
Mflange |
ft-lb |
Appendix B |
|
|
1.45 |
Flange orientation factor |
|
2x4 orientation inertia | |
|
600 |
Ftno2 |
SPF #2 |
|
|
|
1200 |
Ftselect |
Douglas Fir-Larch |
|
|
|
1 |
Cd |
load duration factor |
||
|
538 |
Mweb |
ft-lb |
Appendix B |
|
|
1 |
Note3 |
Factor |
Appendix B Note 3 |
|
|
1.19 |
Note4 |
Factor |
Appendix B Note 4 |
|
|
|
|
|
|
|
|
3231 |
ft-lb |
Allowable moment |
||
The factor of safety for this example for bending moment is 3231/1824 or 1.77 for normal loading. During a wind event, the load duration factor should be 1.6 for a ten-minute wind loading. Dividing the wind loading moment component by 1.6 reduces the total acting moment to 2144 foot-pounds, or a safety factor of 1.5.
Shear load
Acting shear load is simplified to P/2, or 912 pounds without wind loading and 1168 pounds during a wind loading event.
Allowable horizontal shear on a section can be calculated by:
Vh = Fv' It Σts
__________
Q
where
Vh = Allowable total horizontal shear through the panel thickness on the section lbs
Fv' = Allowable plywood shear stress through the panel thickness psi
It = Total moment of inertia about the neutral axis of all parallel-grain material (inch4)
Σts = Total shear thickness of all webs at the section inches
Q = Statical moment about the neutral axis of all parallel-grain material, lying above or below the neutral axis inch3
Q = Q(flanges) + Q(webs)
Q =
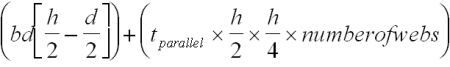
where
b = Breadth of flange (inches)
d = Depth of flange (inches)
h = Depth of header (inches)
tparallel = Total thickness of parallel plies[iv], area square inches per foot
Calculation of the maximum allowable shear is again simplified by using APA’s Design and Fabrication of Glued Plywood-Lumber Beams. Appendix B tables give a preliminary starting point for shear stresses, in the case of this example, 1145 pounds. Adjusting according to Appendix B, note 5, a multiplying factor of 1.8 for 15/32" plywood gives a maximum allowable shear of 2061 pounds. The acting shear stress is clearly within the maximum allowable shear stress.
Approximate deflection
The more accurate calculation for deflection of the wood structural panel box header takes into account the contributions of flange and web explicitly by adding an additional factor based on the shear deflection equation to the general form. The less accurate general form of maximum deflection for a point load located b distance on a simply supported beam of length L is:
![]()
However, for this example, sufficient accuracy will be had by assuming that the point load is in the middle of the beam (worst case) and using this equation:
![]()
where
Δ = maximum deflection in inches
P = Point load in pounds
L = Length of header in inches
E = Modulus of elasticity for flange lumber psi
I = Total moment of inertia about the neutral axis of all parallel-grain material (inches4)
For this example, it will not be necessary to compute the total moment of inertia. The moment of inertia of the flanges alone will be sufficient.
| b | ||
| I (flanges) = | [h3 - (h-2d)3] | |
| 12 |
where
b = Breadth of flange member inches (here 3.5)
d = Depth of flange member inches (here 1.5)
h = Depth of header inches (here 12)
Let P = 1824 pounds, no wind; L = 48 inches; E = 1,300,000 psi, SPF No.2; I = 291 inches4 net flange only
Δ = 0.005 inches
Deflection is an order of magnitude better than L/360.
Additional considerations
Three other considerations are addressed now: lateral stability, end compression, and rolling shear. The ratio of run to depth for the header is less than 5. Under this condition, no lateral bracing is needed.
End compression is present on the 2x4 flanges and
bearing stiffeners. The lumber is SPF No.2 with fiber compression parallel Fc
of 675 psi and perpendicular Fc![]() of
265 psi. Area of the 2x4 is 5.25 square inches. The limiting factor is
perpendicular compression of 1391 pounds allowable. Point load on the header is
1824 pounds, which is divided between the end bearings. End bearings thus have a
factor of safety of 1.5 under normal conditions. Wind loading does not cause the
ends to crush. However, supporting the header eccentrically will shift the
resisting forces, which would not be good at the close end.
of
265 psi. Area of the 2x4 is 5.25 square inches. The limiting factor is
perpendicular compression of 1391 pounds allowable. Point load on the header is
1824 pounds, which is divided between the end bearings. End bearings thus have a
factor of safety of 1.5 under normal conditions. Wind loading does not cause the
ends to crush. However, supporting the header eccentrically will shift the
resisting forces, which would not be good at the close end.
Is end compression a problem in this example? If
the headers are installed to the print and without any modification in the
field, then the design is adequate. Murphy’s Law says otherwise. Replacing SPF
with Southern Pine will increase Fc![]() to
405 psi, and move up allowable compression from 1391 pounds to 2126 pounds. This
resistance is sufficient to handle the entire loading under non-wind conditions.
Previous calculations are affected by the change in FT from 600 to
675, and E from 1,300,000 to 1,600,000, both in the better direction. In order
to increase the likelihood that Southern Pine actually makes it into the header,
it might be helpful to have 2x6 dimensional lumber ripped to 4.5" and dispense
with the plywood spacers, as originally envisioned.
to
405 psi, and move up allowable compression from 1391 pounds to 2126 pounds. This
resistance is sufficient to handle the entire loading under non-wind conditions.
Previous calculations are affected by the change in FT from 600 to
675, and E from 1,300,000 to 1,600,000, both in the better direction. In order
to increase the likelihood that Southern Pine actually makes it into the header,
it might be helpful to have 2x6 dimensional lumber ripped to 4.5" and dispense
with the plywood spacers, as originally envisioned.
End stiffeners must also meet a minimum thickness in order to resist rolling shear.
Minimum thickness = P
_____
2hFs'
where
P = Concentrated load or reaction in pounds
h = Depth of header (inches)
Fs' = Allowable plywood rolling shear stress (psi)[v]
Let P = 1824 (full loading); h = 12; Fs' = 44
Then, minimum thickness is 3.45".
Results
Only a few calculations are needed to prove feasibility of a wood structural panel box header for residential wood-frame construction. For short headers, a point load is a more accurate model than uniform loading as assumed in APA’s Design and Fabrication of Glued Plywood-Lumber Beams.
About the Author
James A. Lacy is a registered professional engineer in Texas. His publications include Systems Engineering Management: Achieving Total Quality, McGraw-Hill, 1992.
List of Works Consulted
APA — The Engineered Wood Association. Design and Fabrication of Glued Plywood-Lumber Beams. Supplement 2. 1992.
APA — The Engineered Wood Association. Plywood Design Specification. 1997.
International Code Council Inc. International Residential Code for One- and Two- Family Dwellings. 2000.
[i]2000 International Residential Code, see Tables R301.2(2) and R301.2(3).
[ii]American Forest and Paper Association. National Design Specification for Wood Construction. CF accounts for smaller size of 2x4 solid-sawn lumber.
[iii]Normal duration of load 1.00; 1.6 for 10 minutes of wind.
[iv]Plywood Design Specification, see Table 1 column 4, and unit conversion by dividing by 12.
[v]Plywood Design Specification, see Table 3, section 3.8.2, and section 3.3.
Article # 0026 TEST QUESTIONS:
1. What main issue(s) controls the structural design of headers?
allowable moment
allowable deflection
allowable shear
All of the above
2. Load-bearing headers distribute forces around ______?
building inspectors
wall openings
windows
All of the above
3. The selection of allowable deflection depend on ______?
code required minimums
interior and exterior finishes
a. and b.
None of the above
4. What is the IRC?
International Residential Construction
International Requirement Committee
International Residential Code
Internal Revenue Commission
5. What is the UBC?
Universal Building Code
Uniform Basic Construction
Ubiquitous Building Committee
Uniform Building Code
6. In this paper, what does SPF stand for?
Specification for Plywood Framing
Spruce-Pine-Fir
Southern Pacific Freight
Southwest Plywood Foundation
7. What is ASD?
Allowable Stress Design
Apparent Stress Displacement
American Standard Design
None of the above
8. In this paper, what does LRFD stand for?
Load and Resistance Factor Design
Larch-Rainer-Fir-Douglas pine
Load Resistant, Fixed Displacement
None of the above
9. What is an effect of replacing SPF with Southern Pine in the above example?
Increases the allowable compression
Decreases the fiber compression, Fc
Increases the loading.
All of the above
10. What is the cross sectional area of 2x4 dimension lumber?
8 in2
6.5 in2
5.25 in2
none of the above
Take a Test Article Library CEEJ Home Submit an Article Contact CEEJ